Шпаргалка по Рекуррентным Нейронным Сетям
Star

Afshine Amidi и Shervine Amidi; Alexandr Parkhomenko и Труш Георгий (Georgy Trush)

Обзор

Архитектура классической RNN Рекуррентные нейронные сети, также известные как RNN, представляют собой класс нейронных сетей, которые позволяют использовать предыдущие выходы в качестве входов, имея скрытые состояния. Обычно они следующие:

Для каждого временного шага $t$ активация $a^{< t >}$ и выход $y^{< t >}$ выражаются следующим образом:

\[\boxed{a^{< t >}=g_1(W_{aa}a^{< t-1 >}+W_{ax}x^{< t >}+b_a)}\quad\textrm{и}\quad\boxed{y^{< t >}=g_2(W_{ya}a^{< t >}+b_y)}\]

где $W_{ax}, W_{aa}, W_{ya}, b_a, b_y$ являются коэффициентами, которые являются одинаковыми для всех ячеек RNN во времени, и функциями активации $g_1, g_2$ .

Плюсы и минусы типичной архитектуры RNN перечислены в таблице ниже:

Преимущества	Недостатки
• Возможность обработки входа любой длины • Размер модели не увеличивается с размером входных данных • При расчетах учитывается историческая информация • Веса распределяются во времени	• Вычисления идут медленно • Сложность доступа к очень давней информации • Невозможно рассмотреть какие-либо будущие входные данные для текущего состояния

Применение RNN Модели RNN в основном используются в области обработки естественного языка и распознавания речи. Различные приложения приведены в таблице ниже:

Тип RNN	Иллюстрация	Пример
One-to-one $T_x=T_y=1$		Классическая нейронная сеть
One-to-many $T_x=1, T_y>1$		Генерация музыки
Many-to-one $T_x>1, T_y=1$		Определение эмоциональной окраски, Классификация эмоций (Sentiment classification)
Many-to-many $T_x=T_y$		Распознавание именованных сущностей (Name entity recognition NER)
Many-to-many $T_x\neq T_y$		Машинный перевод

Функция потерь В случае рекуррентной нейронной сети функция потерь $\mathcal{L}$ всех временных шагов определяется на основе значений функции потерь на каждом временном шаге следующим образом:

\[\boxed{\mathcal{L}(\widehat{y},y)=\sum_{t=1}^{T_y}\mathcal{L}(\widehat{y}^{< t >},y^{< t >})}\]

Обратное распространение ошибки во времени Обратное распространение выполняется в каждый момент времени. На временном шаге $T$ производная потерь $\mathcal{L}$ по матрице весов $W$ выражается следующим образом:

\[\boxed{\frac{\partial \mathcal{L}^{(T)}}{\partial W}=\sum_{t=1}^T\left.\frac{\partial\mathcal{L}^{(T)}}{\partial W}\right|_{(t)}}\]

Обработка долгосрочных зависимостей

Часто используемые функции активации Наиболее распространенные функции активации, используемые в модулях RNN, описаны ниже:

Sigmoid	Tanh	RELU
$\displaystyle g(z)=\frac{1}{1+e^{-z}}$	$\displaystyle g(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$	$\displaystyle g(z)=\max(0,z)$

Исчезающий/взрывающийся градиент Явления исчезающих и взрывных градиентов часто встречаются в контексте RNN. Причина, по которой они происходят, заключается в том, что трудно зафиксировать долгосрочные зависимости из-за мультипликативного градиента, который может экспоненциально уменьшаться/увеличиваться по отношению к количеству слоев.

Отсечение градиента это метод, используемый для решения проблемы взрывных градиентов, иногда возникающей при выполнении обратного распространения ошибки. Ограничивая максимальное значение градиента, это явление контролируется на практике.

Типы вентилей чтобы решить проблему исчезающего градиента, в некоторых типах RNN используются специфичные вентили, которые обычно имеют четко определенную цель. Обычно они обозначаются $\Gamma$ и равны:

\[\boxed{\Gamma=\sigma(Wx^{< t >}+Ua^{< t-1 >}+b)}\]

где $W, U, b$ ― коэффициенты, относящиеся к вентилю, а $\sigma$ - функция сигмоиды. Основные из них приведены в таблице ниже:

Тип вентиля	Роль	Используется в
Update gate $\Gamma_u$	Насколько прошлое должно иметь значение сейчас?	GRU, LSTM
Relevance gate $\Gamma_r$	Отбросить предыдущую информацию?	GRU, LSTM
Forget gate $\Gamma_f$	Стереть ячейку или нет?	LSTM
Output gate $\Gamma_o$	Насколько раскрыть ячейку?	LSTM

GRU/LSTM Вентильный Рекуррентный Блок (Gated Recurrent Unit, GRU) и Блок с Долгой Краткосрочной Памятью (Long Short-Term Memory units, LSTM) имеет дело с проблемой исчезающего градиента, с которой сталкиваются традиционные RNN, причем LSTM является обобщением GRU. Ниже представлена таблица, в которой перечислены характеризующие уравнения каждой архитектуры:

Характеристика	Gated Recurrent Unit (GRU)	Long Short-Term Memory (LSTM)
$\tilde{c}^{< t >}$	$\textrm{tanh}(W_c[\Gamma_r\star a^{< t-1 >},x^{< t >}]+b_c)$	$\textrm{tanh}(W_c[\Gamma_r\star a^{< t-1 >},x^{< t >}]+b_c)$
$c^{< t >}$	$\Gamma_u\star\tilde{c}^{< t >}+(1-\Gamma_u)\star c^{< t-1 >}$	$\Gamma_u\star\tilde{c}^{< t >}+\Gamma_f\star c^{< t-1 >}$
$a^{< t >}$	$c^{< t >}$	$\Gamma_o\star c^{< t >}$
Зависимости

Примечание: знак $\star$ означает поэлементное умножение двух векторов.

Варианты RNN В таблице ниже перечислены другие часто используемые архитектуры RNN:

Bidirectional (BRNN)	Deep (DRNN)

Представление обучающих слов

В этом разделе мы обозначаем словарь $V$ и его размер $|V|$.

Мотивация и обозначения

Методы представления два основных способа представления слов подытожены в таблице ниже:

One-hot представление	Представления слов

• Обозначено $o_w$ • Наивный подход, нет информации о сходстве	• Обозначено $e_w$ • Учитывает сходство слов

Матрица представления (embedding matrix) для данного слова $w$ матрица представления $E$ является матрицей, которая отображает свое one-hot представление $o_w$ на его представление $e_w$ следующим образом:

\[\boxed{e_w=Eo_w}\]

Примечание: получить матрицу представлений можно путем обучения моделей целевого/контекстного правдоподобия.

Векторные представления слов

Word2vec это фреймворк, предназначенный для получения представлений слов путем оценки вероятности того, что данное слово окружено другими словами. Популярные модели включают Skip-gram, Negative sampling и CBoW.

Skip-gram Модель skip-gram word2vec - это алгоритм обучения с учителем, который выучивает представления слов, оценивая правдоподобие того, что любое заданное целевое слово $t$ встречается с контекстным словом $c$. Обозначим $\theta_t$ параметр, связанный с $t$, вероятность $P(t|c)$ определяется выражением:

\[\boxed{P(t|c)=\frac{\exp(\theta_t^Te_c)}{\displaystyle\sum_{j=1}^{|V|}\exp(\theta_j^Te_c)}}\]

Примечание: суммирование по всему словарю в знаменателе части softmax делает эту модель дорогостоящей в вычислительном отношении. CBOW - это еще одна модель word2vec, использующая окружающие слова для предсказания данного слова.

Negative sampling Отрицательная выборка - набор бинарных классификаторов, использующих логистические регрессии, целью которых является оценка того, как данный контекст и заданные целевые слова могут появляться одновременно, при этом модели обучаются на наборах из $k$ отрицательных примеров и 1 положительного примера. Учитывая контекстное слово $c$ и целевое слово $t$, прогноз выражается следующим образом:

\[\boxed{P(y=1|c,t)=\sigma(\theta_t^Te_c)}\]

Примечание: этот метод менее затратен с точки зрения вычислений, чем модель скип-граммы.

GloVe Модель GloVe, сокращение от глобальных векторов для представления слов, является методом получения представлений слов, который использует матрицу совпадения $X$, где каждый $X_{i,j}$ обозначает количество раз, когда цель $i$ встречалась с контекстом $j$. Его функция стоимости $J$ выглядит следующим образом:

\[\boxed{J(\theta)=\frac{1}{2}\sum_{i,j=1}^{|V|}f(X_{ij})(\theta_i^Te_j+b_i+b_j'-\log(X_{ij}))^2}\]

где $f$ - такая взвешивающая функция, что $X_{i,j}=0\Longrightarrow f(X_{i,j})=0$.
Учитывая симметрию, которую играют $e$ и $\theta$ в этой модели, последнее представление слов $e_w^{(\textrm{final})}$ задается выражением:

\[\boxed{e_w^{(\textrm{final})}=\frac{e_w+\theta_w}{2}}\]

Примечание: отдельные компоненты векторов представлений слов не обязательно поддаются интерпретации.

Сравнение слов

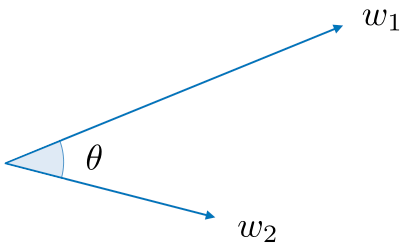
Косинусное сходство косинусное сходство между словами $w_1$ и $w_2$ выражается следующим образом:

\[\boxed{\textrm{similarity}=\frac{w_1\cdot w_2}{||w_1||\textrm{ }||w_2||}=\cos(\theta)}\]

Примечание: $\theta$ - угол между словами $w_1$ и $w_2$.

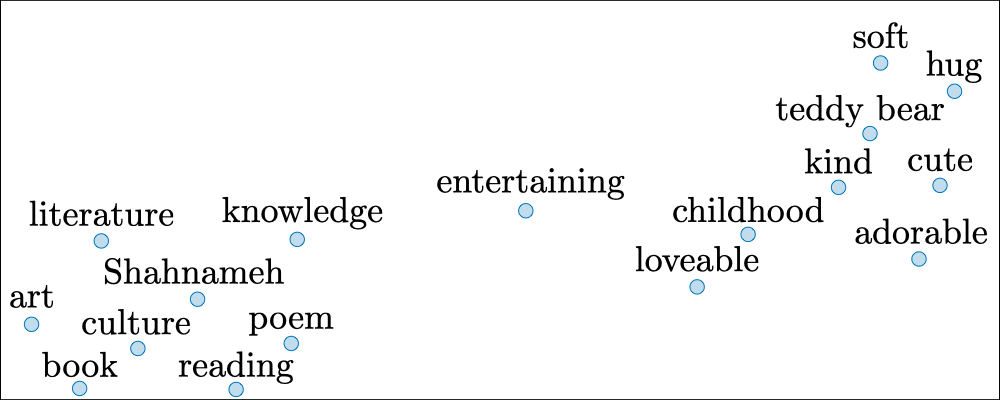
$t$-SNE $t$-распределенное стохастическое соседнее представление ($t$-distributed Stochastic Neighbor Embedding, $t$-SNE) - это метод, направленный на сокращение представлений большой размерности в пространство меньшей размерности. На практике он обычно используется для визуализации векторов слов в 2D-пространстве.

Языковая модель

Обзор языковая модель предназначена для оценки вероятности предложения $P(y)$.

Модель $n$-gram эта модель представляет собой наивный подход, направленный на количественную оценку вероятности того, что выражение появляется в корпусе, путем подсчета его количества появлений в обучающих данных.

Метрика Perplexity Perplexity (Недоумение) - языковые модели обычно оцениваются с помощью метрики Perplexity, также известной как PP, которую можно интерпретировать как обратную вероятность набора данных, нормализованную на количество слов $T$. Perplexity таково, что чем оно ниже, тем лучше, и определяется следующим образом:

\[\boxed{\textrm{PP}=\prod_{t=1}^T\left(\frac{1}{\sum_{j=1}^{|V|}y_j^{(t)}\cdot \widehat{y}_j^{(t)}}\right)^{\frac{1}{T}}}\]

Примечание: PP обычно используется в $t$-SNE.

Машинный перевод

Обзор модель машинного перевода похожа на языковую модель, за исключением того, что перед ней размещена сеть кодировщика. По этой причине её иногда называют условной моделью языка.

Цель состоит в том, чтобы найти такое предложение $y$, что:

\[\boxed{y=\underset{y^{< 1 >}, ..., y^{< T_y >}}{\textrm{arg max}}P(y^{< 1 >},...,y^{< T_y >}|x)}\]

Лучевой поиск это алгоритм эвристического поиска, используемый в машинном переводе и распознавании речи для поиска наиболее вероятного предложения $y$ при вводе $x$.

• Шаг 1: Найти top $B$ наиболее вероятных слов $y^{< 1 >}$
• Шаг 2: Вычислить условные вероятности $y^{< k >}|x,y^{< 1 >},...,y^{< k-1 >}$
• Шаг 3: Сохранить top $B$ комбинации $x,y^{< 1>},...,y^{< k >}$

• Шаг 4: Завершить процесс на стоп-слове

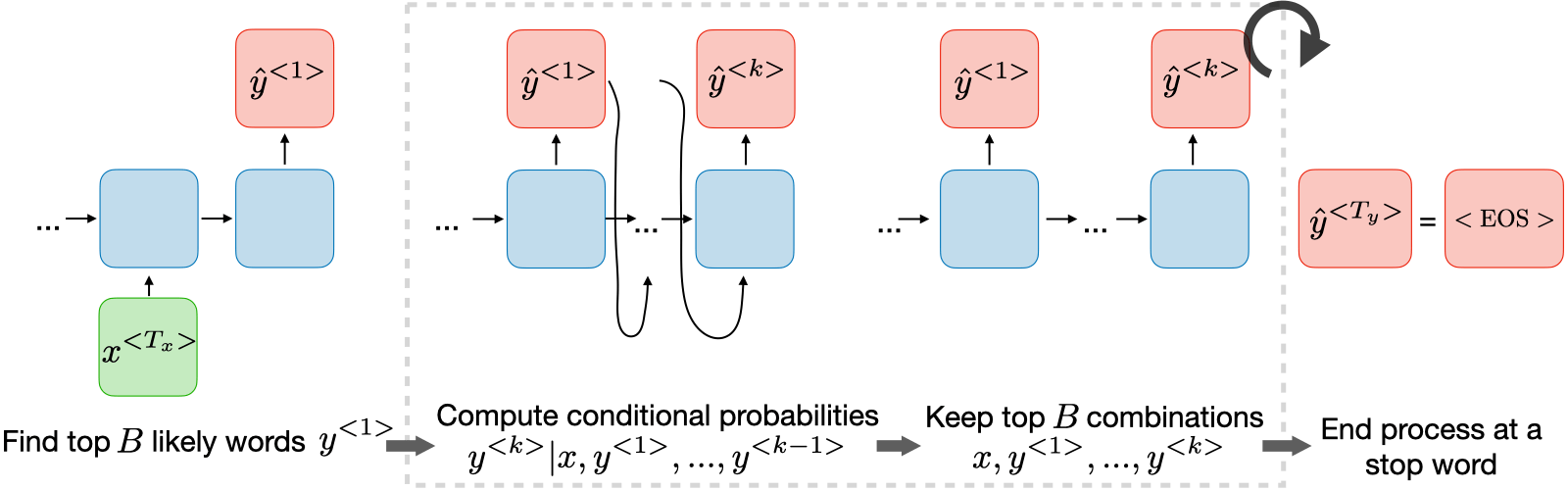
Примечание: если ширина луча установлена на 1, то это равносильно наивному жадному поиску.

Ширина луча Ширина луча $B$ является параметром лучевого поиска. Большие значения $B$ дают лучший результат, но с меньшей производительностью и увеличенным объёмом памяти. Маленькие значения $B$ приводят к худшим результатам, но требуют меньших вычислительных затрат. Стандартное значение $B$ составляет около 10.

Нормализация длины Чтобы улучшить численную стабильность, лучевой поиск обычно применяется к следующей нормализованной цели, часто называемой нормализованной целью логарифмического правдоподобия, определяемой как:

\[\boxed{\textrm{Objective } = \frac{1}{T_y^\alpha}\sum_{t=1}^{T_y}\log\Big[p(y^{< t >}|x,y^{< 1 >}, ..., y^{< t-1 >})\Big]}\]

Примечание: параметр $\alpha$ можно рассматривать как смягчитель, и его значение обычно составляет от 0.5 до 1.

Анализ ошибок При получении предсказанного перевода $\widehat{y}$, который является плохим, можно задаться вопросом, почему мы не получили хороший перевод $y^*$ , выполнив следующий анализ ошибок:

Случай	$P(y^*\|x)>P(\widehat{y}\|x)$	$P(y^*\|x)\leqslant P(\widehat{y}\|x)$
Первопричина	Ошибка лучевого поиска	Неисправность RNN
Исправления	Увеличить ширину луча	• Попробовать другую архитектуру • Регуляризировать • Взять больше данных

Метрика BLEU оценка дублера для двуязычной оценки (bilingual evaluation understudy, BLEU) количественно определяет, насколько хорош машинный перевод, путем вычисления оценки сходства на основе точности $n$-грамм. Это определяется следующим образом:

\[\boxed{\textrm{bleu score}=\exp\left(\frac{1}{n}\sum_{k=1}^np_k\right)}\]

где $p_n$ - это оценка по $n$-граммам, определяемая только следующим образом:

\[p_n=\frac{\displaystyle\sum_{\textrm{n-gram}\in\widehat{y}}\textrm{count}_{\textrm{clip}}(\textrm{n-gram})}{\displaystyle\sum_{\textrm{n-gram}\in\widehat{y}}\textrm{count}(\textrm{n-gram})}\]

Примечание: к коротким предсказанным переводам может применяться штраф за краткость, чтобы предотвратить искусственно завышенную оценку BLEU.

Внимание

Модель внимания эта модель позволяет RNN обращать внимание на определенные части входных данных, которые считаются важными, что на практике улучшает производительность полученной модели. Обозначим $\alpha^{< t, t'>}$ количество внимания, которое выход $y^{< t >}$ должен уделять активации $a^{< t' >}$ и $c^{< t >}$ контексту в момент времени $t$, у нас есть:

\[\boxed{c^{< t >}=\sum_{t'}\alpha^{< t, t' >}a^{< t' >}}\quad\textrm{with}\quad\sum_{t'}\alpha^{< t,t' >}=1\]

Примечание: оценки внимания обычно используются при добавлении субтитров к изображениям и машинном переводе.

Вес внимания количество внимания, которое выход $y^{< t >}$ должен уделять активации $a^{< t' >}$, задается выражением $\alpha^{< t,t' >}$, вычисляемым следующим образом:

\[\boxed{\alpha^{< t,t' >}=\frac{\exp(e^{< t,t' >})}{\displaystyle\sum_{t''=1}^{T_x}\exp(e^{< t,t'' >})}}\]

Примечание: сложность вычислений квадратична относительно $T_x$.

Шпаргалка по Рекуррентным Нейронным Сетям Star